
Welcome to Abacus Lesson 9!
In our past lessons, we’ve explored both addition and subtraction, relying heavily on the upper bead “5” for efficient calculations. This upper bead holds particular importance because each column can only accommodate 4 lower beads, demanding a strategic approach for smooth operation.
Introducing the friend approach, we’ve become acquainted with pairs of friends that combine to make “5” (complements of 5). With this approach, we can avoid the complexity of calculating excess or difference when borrowing too much by simply adding or subtracting the value of its friend. Mastering the use of “5” is key, and understanding the sequence in which we deploy it greatly enhances our speed.
Now, in this lesson, we’re introducing another friend approach: “making 10 together.” As the abacus functions on a place value system, we often encounter scenarios where we need to carry over or borrow from the next digit, especially with multi-digit numbers. There are 5 pairs of friends that work together to make “10,” and it’s crucial for us to become proficient in handling them. While memorizing these 5 pairs may seem daunting at first, it becomes much quicker with practice. Ready to dive in and explore? Let’s get started!

Addition with Carrying Over
Adding with carrying over on the abacus can be a bit challenging for some. However, with the friend approach, though applied differently, the concept stays the same. There are special pairs that team up to make “10” together. When we carry over to the next digit, it’s important to subtract the excess we added. By using the friend approach, we can easily recognize the excess and finish the calculation.
Adding with carrying over on the abacus can be a bit challenging for some. However, with the friend approach, though applied differently, the concept stays the same. There are special pairs that team up to make “10” together. When we carry over to the next digit, it’s important to subtract the excess difference we added. By using the friend approach, we can easily recognize the difference and finish the calculation.
Take a look at the table below, which illustrates the pairs of friends that combine to make 10 together.
Similar to the pairs that make “5” together (5-complement), these sets of friends also team up to make “10” together (10-complement).
When we carry over to the next digit, there’s always an excess that needs to be subtracted. While we can calculate this excess, remembering its pair makes it easier—it is essentially the excess itself, saving us the need for additional calculations.
It’s a quicker way to go about it.
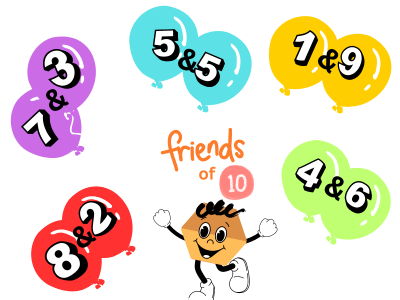

How to apply the friend approach when carrying over
If you wish to add a number in a particular column, such as the ones column, but there’s no space for additional beads, what’s the solution? You carry over to the next digit, which is the tens place column. But remember, when you do this, you’ll need to subtract the excess you added.
For example, let’s say you’re adding 2 + 9. You’ll need to carry over 1 to the tens column and then subtract 1, which is the excess you added.
Below, you’ll find the 9 combinations that make 10 together. Although it might seem like a lot, there are actually only 5 pairs: 1 & 9, 2 & 8, 3 & 7, 4 & 6, and 5 & 5. By memorizing these pairs, you’ll be able to apply the friend approach immediately. It might be helpful to print them out alongside “the friends that make 5 together” and keep them nearby while you work on the abacus


When we use the friend approach to borrow the upper bead “5”, all the calculaitons were done without carrying over. But sometimes, the upper bead “5” isn’t available. In those situations, we have to carry over 1 to the next higher place value.
Let’s take a look at some examples below to see how the friend approach, which makes 10 together, comes into play.

The Friend Approach for Addition with Carry Over :
1 & 9
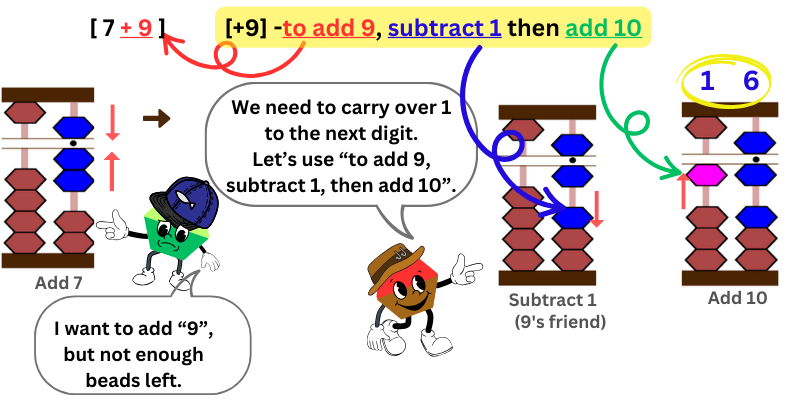
We will start by adding “7” on ones column first.
Next, we want to add “9,” but with only two lower beads remaining, we can’t add to the same ones place column.
What’s the solution?
Refer to the table of “Friend Approach – 10 Complements.” Look for the entry “to add 9.”
It says, “To add 9, subtract 1, then add 10.”
While carrying over 1 to the tens place column, it’s important to subtract 1 first and then add 10.
Count the number of beads attached at the bar. It’s 16. Thus, 7+9=16.

The Friend Approach for Addition with Carry Over :
6 & 4
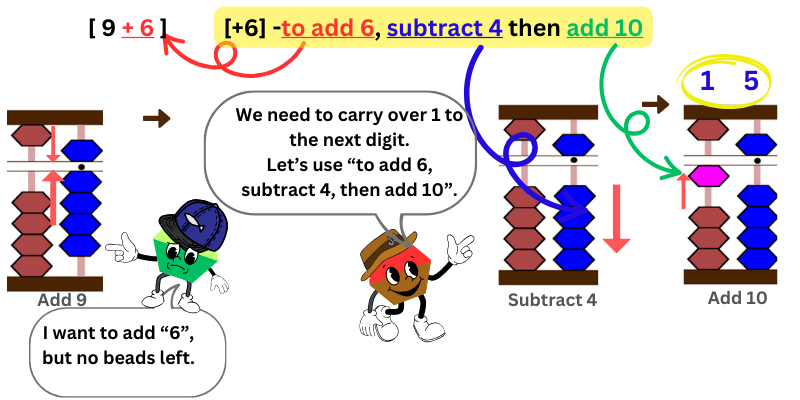
We will start by adding “9” on ones column first.
Next, we want to add “6,” but no lower beads remain. We can’t add to the same ones place column.
What’s the solution?
We can apply the friend approach – 10 complements. Look for the entry “to add 6.” It says, “To add 6, subtract 4, then add 10.” While carrying over 1 to the tens place column, it’s important to subtract 4 first and then add 10.
Count the number of beads attached at the bar. It’s 16. Thus, 9+6=16.

The Friend Approach for Addition with Carry Over :
8 & 5
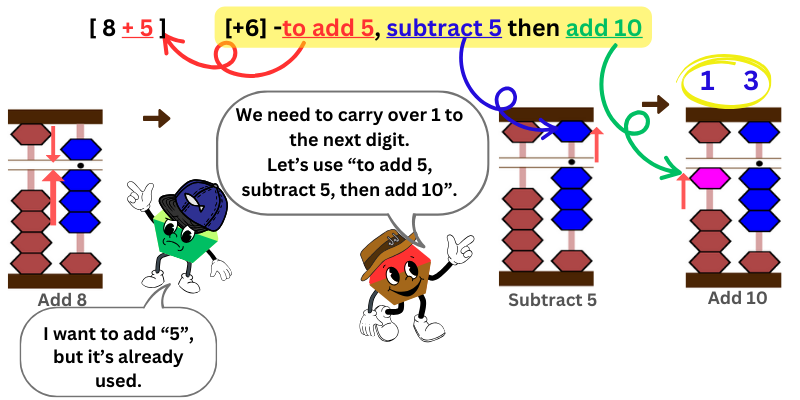
We will start by adding “8” on ones column first.
Next, we want to add “5,” but the upper bead on ones place column has already been used. So, we can’t add to the same ones place column.
What’s the solution?
We can apply the friend approach – Complements of 10. Look for the entry “to add 5.” It says, “To add 5, subtract 5, then add 10.” While carrying over 1 to the tens place column, it’s important to subtract 5 first and then add 10.
Count the number of beads attached at the bar. It’s 13. Thus, 8+5=13.

I hope you’re grasping the concept of carrying over on the abacus using the friend approach. Use the printouts of the charts for both “5” and “10” friends while practicing until you feel comfortable working on the abacus without them.

Practice Questions
Work through all the worksheet or video problems multiple times until you feel confident with addition with carrying over using the friend approach. Consistent practice will enhance your skills.
Click the green button below to access the printable worksheets.



In this lesson, we explored addition with carrying over, focusing on the ones column. The method we used, known as the friend approach or “making 10 together,” applies similarly to multi-digit additions. For example, when adding 70 + 90, you carry over 1 to the next higher place value, which is 100, then subtract 10 (its friend). Understanding this friend approach for making 10 together is just as crucial as the one for making 5 together.
In our next lesson, we’ll delve into using the friend approach for subtraction. To aid your practice, please print out the chart for making 5 and 10 together and keep it handy until you’ve memorized all the pairs.

