
Welcome to Abacus Lesson 8!
In our last lesson, we introduced a helpful strategy known as the friend approach. When working with a Japanese abacus, we often need to borrow from the upper bead because we have a limited number of lower beads. But here’s the catch – when we borrow, we also have to subtract the excess that we borrowed too much. That’s where the friend approach comes in handy.
There are only two pairs of friends that make 5 together, known as complements of 5. And there are just four simple steps to follow when using the friend approach. Once you memorize them, you won’t need to do any extra math to figure out the excess. You simply subtract the friend as the excess for addition.
In this lesson, we’ll guide you through using the friend approach for subtraction. Our trusty friends remain the same: 1 and 4, and 2 and 3. But here’s the twist – while we subtracted the excess after borrowing the upper bead for addition, for subtraction, we add the difference first and then subtract the upper bead. The approach may be a little different, but the concept remains unchanged.
Ready to dive into subtraction using the friend approach? As we’ve emphasized before, this method, known as the complement of 5, is key to mastering the abacus. Take the time to understand it well and practice frequently, so you can commit it to memory and use it confidently

The Friend Approach for Sbubtraction
Although the pairs of friends (complements of 5) remain the same, we apply them a little differently for subtraction.
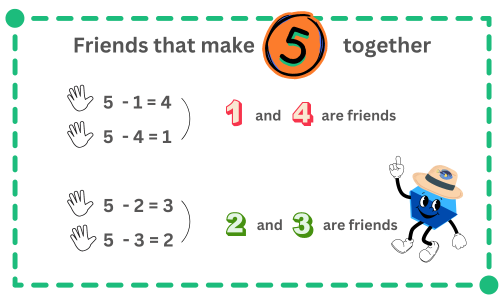
In subtraction, we still rely on our trusty pairs of friends that make 5 together: 1 & 4, and 2 & 3 (complements of 5).
But here’s the twist: when subtracting, we use them a bit differently. Let’s consider 8 – 4 as an example. In abacus terms, 8 is represented by 1 upper bead and 3 lower beads, while 4 corresponds to 4 lower beads. Since we can’t subtract 4 lower beads from 3, we need to borrow from the upper bead “5”. Now, here’s where the difference lies: instead of subtracting the upper bead “5” first, we add the difference “1” first, then subtract “5”. This difference of “1” is the friend of “4”. So, unlike in addition where we first add the upper bead “5” and then subtract the excess, in subtraction, we add the difference (friend) first and then subtract “5”. The order may be different, but the concept remains the same.
The illustration on the right gives you a clear idea of how the friend approach works for subtraction.
For example, let’s look at the first instruction, “To subtract 1.” If you need to subtract 1 on the abacus but don’t have any beads in the lower column to subtract, and the upper bead “5” is available, you add 4 (the friend of 1) and then subtract 5.
Now, consider the second instruction, “To subtract 2.” If there are no beads available to subtract in the lower column and the upper bead “5” is present, you add 3 (the friend of 2) and then subtract 5.
This same principle applies when subtracting 3. If you can’t subtract 3 in the lower column, you add 2 (the friend of 3) and then subtract 5.
Lastly, when subtracting 4, and there are no beads available in the lower column, you add 1 (the friend of 4) and then subtract 5.
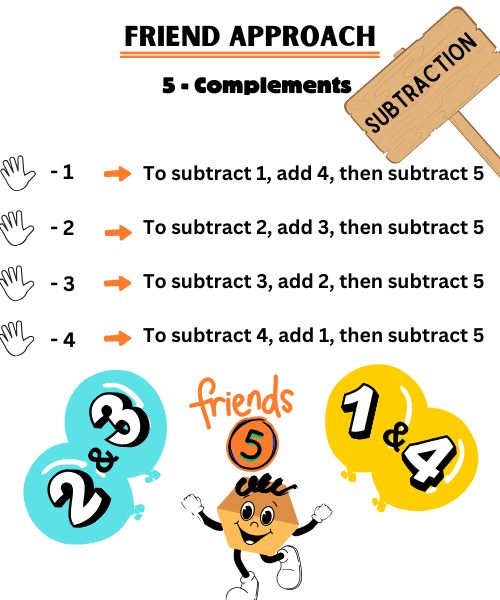

Do you notice the difference between addition and subtraction when using the friend approach? In both cases, we rely on the upper bead “5,” but the way we carry out the operations differs:
For addition, we add the upper bead “5” first and then subtract the excess (the friend).
For subtraction, however, we add the difference (the friend) first and then subtract the upper bead “5”.
It might seem a bit confusing at first, but once you memorize these steps, you’ll find them easy to use.

Let’s put the friend approach into practice with some examples below to understand how it works for subtraction.
The Friend Approach for Subtraction : 1 & 4
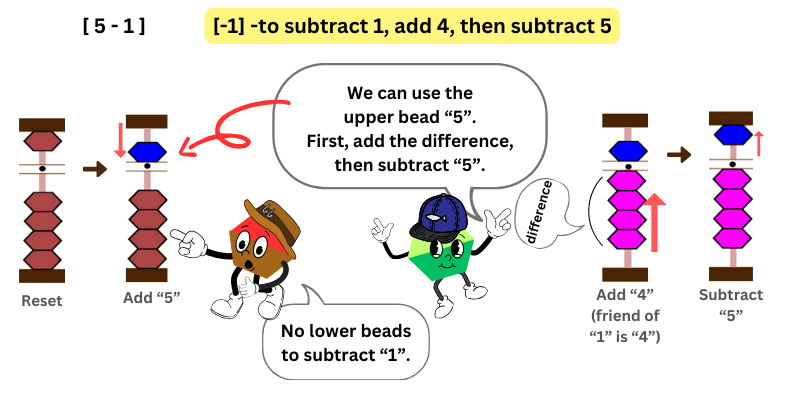
In this example, we want to subtract 5 – 1. First, we add 5 by moving the upper bead towards the bar. But when it’s time to subtract 1, there’s no lower bead to take away.
So, we borrow the upper bead “5”. Since we only need to subtract 1, we add its friend, 4 (the difference that we subtract too much).
Using the friend approach, we can avoid calculating the difference.
For instance, in this example, you want to subtract 1. What is the next phrase?
To subtract 1, add 4, then subtract 5
Therefore, when you want to subtract 1 but no bead available, add its friend 4, then subtract 5.
Did you get an idea how the friend approach works for subtraction? Although we use the same pairs of friend that make 5 together, we apply them differently.
Use the Friend Approach for subtraction if:
- There aren’t enough lower beads to subtract, AND
- The upper bead “5” is available
If the above two conditions are TRUE, then
3. Add its friend, then subtract the upper bead “5”.
Let’s take a look at next example [6 – 2]. Just follow the step if the two conditions above are met.
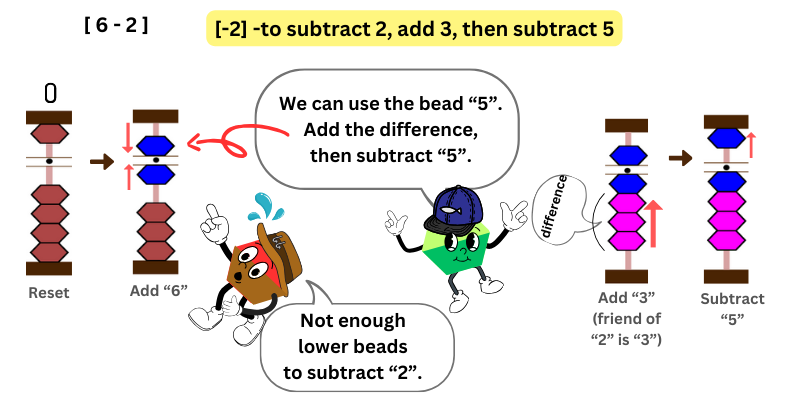
In this example, we want to subtract 6 – 2 We first add 6 by moving the upper bead and 1 lower bead towards the bar.
Then, we want to subtract 2. Oh no! There is no lower bead to subtract 2. What are we going to do?
The upper bead “5” is available, and therefore, we can borrow the upper bead “5”.
Since we only needed to subtract 2, not 5, we should add the difference (its friend) that we subtract too much. The friend of 2 is 3.
For instance, in this example, you want to subtract 2. What is the next phrase?
To subtract 2, add 3, then subtract 5
Therefore, when you want to subtract 2 but no bead available in the lower column, add its friend 3, then subtract 5.
I hope you don’t get confused about the order in which we apply the friend. We add the friend first and then subtract the upper bead.

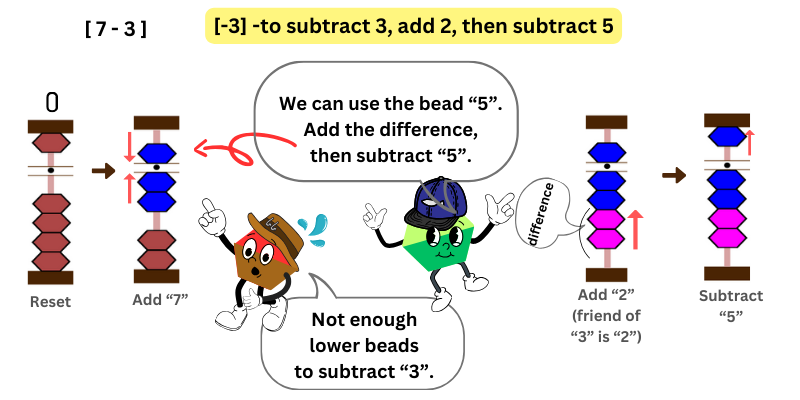
In this example, we subtract 7 – 3. We first add 7 by moving the upper bead and 2 lower beads towards the bar.
Then, we want to subtract 3. However, there are not enough lower beads to subtract 3.
Since the upper bead “5” is available, so we can borrow it. We only need to subtract 3, not 5, so we should add the difference (its friend) that we subtract too much.
If you use the friend approach, you don’t need to calculate the difference -simply add its friend. The friend of 3 is 2.
For instance, in this example, you want to subtract 3. What is the next phrase?
To subtract 3, add 2, then subtract 5
Therefore, when you want to subtract 3 but no bead available, add its friend 2, then subtract 5.
Getting used to the order: add friend first, then subtract 5? Let’s try one more example.

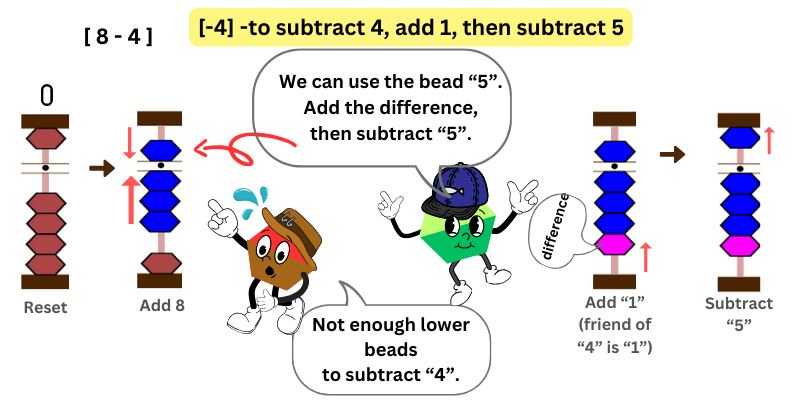
In this example, we want to subtract 8 – 4. We first add 8 by moving the upper bead and 3 lower beads towards the bar.
Then, we want to subtract 4. However, there are not enough lower beads to subtract 4.
Since the upper bead “5” is available, we borrow it.
We first add the difference (its friend) then subtract the upper bead “5”. The friend of 4 is 1.
For instance, in this example, you want to subtract 4. What is the next phrase?
To subtract 4, add 1, then subtract 5
Therefore, when you want to subtract 4 but no bead available, add the friend 1, then subtract 5.

The Friend Approach : Multi-digit
Let’s try out how the friend approach works for multi-digit subtraction.

In this example, we want to subtract 78 -34. As we have learned multi-digit number addition and subtraction, always begin with the one having the highest place value. In this example, start with the tens place column.
The first number is 78. Add 70 on the tens place column first, then add 8 on the ones place column.
Then, we want to subtract 34 from 78. Though we want to subtract 30 first (higher place value), there are no enough lower beads in the tens column but the upper bead 50 is available. Therefore, we can apply the friend approach “to subtract 3, add 2 then subtract 5 ”
For instance, in the tens column, add 20, then subtract 50.
Then moving onto the ones place column, we want to subtract 4 but there aren’t enough beads available. Since the upper bead 5 is available, we can use the friend approach “to subtract 4, add 1, then subtract 5“.
For instance, In the ones column, add 1, then subtract 5.
Count the numbers attached at the bar. It’s 44. 78 – 34 = 44.

Please watch the lesson videos below to strengthen your understanding of the friend approach for subtraction.
Video Lessons (Friend Approach for Subtraction)

Practice Questions
Work through all the worksheet or video problems multiple times until you feel confident with subtraction using the friend approach. Consistent practice will enhance your skills.
Click the green button below to access the printable worksheets.
Click below to access the video practice questions.



In this lesson, we explored the friend approach for subtraction, where certain pairs work together to make 5: 1 and 4, and 2 and 3. These pairs are the same as those used in addition, but their application differs in subtraction. This method becomes useful when you lack lower beads for subtraction but still have the upper bead “5” available. We first add the difference (the friend of the number being subtracted) and then subtract the upper bead “5”. Practice addition and subtraction using this approach to become comfortable with it. In the next lesson, we’ll delve into another important friend approach: making 10 together
You can find the friend approach sheet in PDF format on the worksheet page. Print it out and keep it nearby so you can refer to it while you’re working with the abacus.

