
Welcome to Abacus Lesson 7!
In our previous lessons, we’ve picked up the knack for adding and subtracting with an abacus. Whether it’s single-digit or multi-digit numbers, we’ve got the steps down pat. The key is to spot the right place for each number and start adding from the higher value.
While we’ve dealt with multi-digit numbers, we’ve kept things simple without any need for carrying over or borrowing. Our focus was on straightforward calculations, no fancy tricks required. But here’s a heads-up: in Japanese abacus techniques, using the upper bead “5” or carrying over to the next place value becomes is crucial for more advanced calculations.
Getting comfortable with this upper bead is the first challenge for learning abacus. In today’s lesson, we’ll delve into it using a friendly approach called “Friends that make 5 together” – finding complements of 5. Ready to explore this new technique? Let’s jump in!

The Friend Approach for Addition
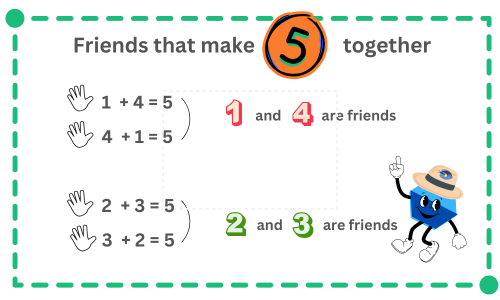
The friend approach is a handy way to find complementary numbers when using the abacus. It’s all about remembering those “other numbers” or “complementary numbers” when we run out of beads and need to borrow “5”. Picture this: You have three lower beads, but you want to add three more, and there’s only one bead left in the lower column. What now? You borrow “5” and then give it back once you’re done.
There are only two pairs of friends who add up to 5 together: 2 and 3, and 1 and 4. By thinking of them as friends, you won’t have to calculate the difference every time. Just subtract your friend! This trick is easy to remember and essential for mastering the abacus.
The illustration on the right demonstrates how the friend approach works in practice.
For instance, the first instruction says “add 1.” This means that when you wish to add 1 on the abacus, but there are no beads available to add in the lower section and the upper bead “5” is open, you add a 5-bead and then subtract 4 (the friend of “1”).
Let’s take a look at the second instruction. It says “add 2” on the abacus. If there are no beads available to add in the lower section and the upper bead “5” is open, you add a 5-bead, then subtract 3 (the friend of “2”).
The same principle applies when adding 3. If there’s no option to add 3 in the lower section, add 5 and then subtract 2 (the friend of 3).
Finally, the same principle holds true when adding 4. If there’s no option to add 4 in the lower section, add 5 and then subtract 1 (the friend of 4).


Sometimes, you’ll find yourself needing to borrow the upper bead 5. If it’s available, you can use it, but you’ll have to give back what you’ve added too much. This is where the friend approach comes in handy. If you remember who makes 5 together (5-complements), you won’t have to figure out the excess. You can quickly spot the excess (the friend) and take it away.
Since the “Friends that make 5 together” approach is so important, we’ll go through each step carefully to make sure you understand it well.
Now, there are two pairs of friends that make 5 together: 1 & 4, and 2 & 3. Let’s start with the friends of 1 & 4.

The Friend Approach for Addition: 1 & 4
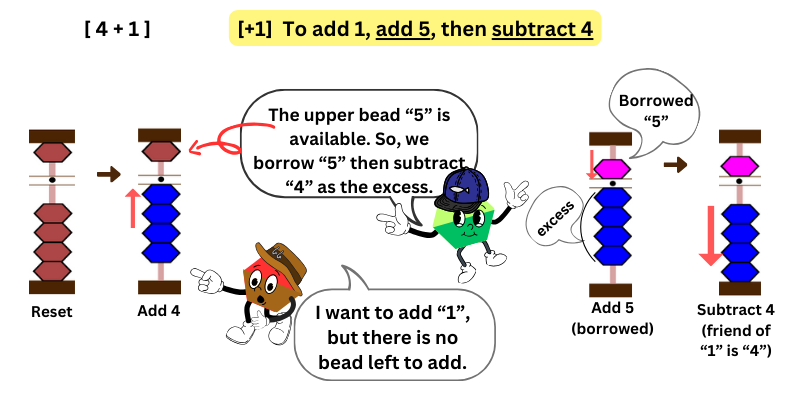
In this example, we want add 4 + 1. We first add 4 by moving 4 lower beads towards the bar – no problem. Then, we want to add 1,but here is no lower bead available (all used up)! What are we going to do? The upper bead “5” is open, and we can borrow the upper bead “5”.
It’s not done yet. Since we only needed to add 1, we should subtract the excess.
How do we calculate the excess? We can get the excess by 5 (borrowed) – 1(needed this much). It’s 4.
However, if you use the friend approach, you don’t need to calculate the excess -simply subtract its friend.
For instance, in this example, you want to add 1. What is the next phrase?
To add 1, add5, then subtract 4
Therefore, when you want to add 1 but there are not enough lower beads, add (borrow) the upper bead 5, then subtract 4.
Use the Friend Approach for addition if:
- There aren’t enough lower beads to add, AND
- The upper bead “5” is available
If the above two conditions are TRUE, then
3. Add (borrow) the upper bead “5”, then subtract its friend.
Let’s take a look at this example [3 + 4]. Just follow the step if the two conditions above are met.
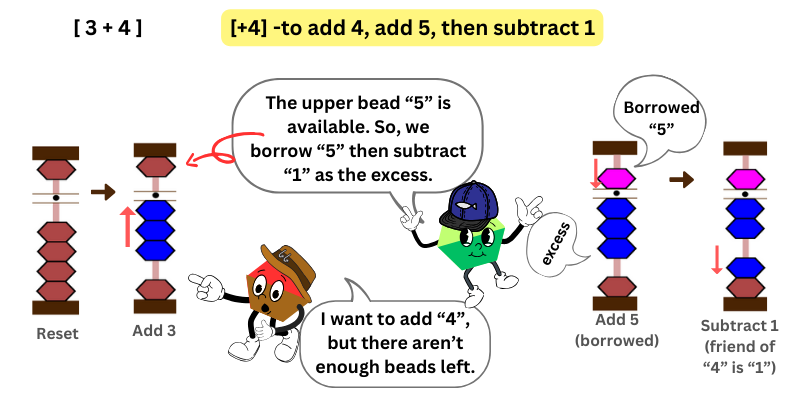

In this example, we want to add 3 + 4. We add 3 by moving 3 lower beads towards the bar.
We want to add 4 next, but there aren’t enough lower beads available (only 1 lower bead).
What we want to do is to see if the upper bead 5 is available.
Yes, it’s available! Therefore, we borrow the upper bead 5, then we subtract the excess.
If you apply the friend approach, you can identify the excess right away!
Who is 4’s friend? It’s 1. Thus, you subtract 1 and count the number of beads left on the abacus. That’s the answer.
For instance, in this example, you want to add 4. What is the next phrase?
To add 4, add 5, then subtract 1
Therefore, when you wanted to add 4 but not enough beads available, add (borrow) the upper bead 5, then subtract 1.
The friend approach is so much faster than calculation.

The Friend Approach : 2 & 3
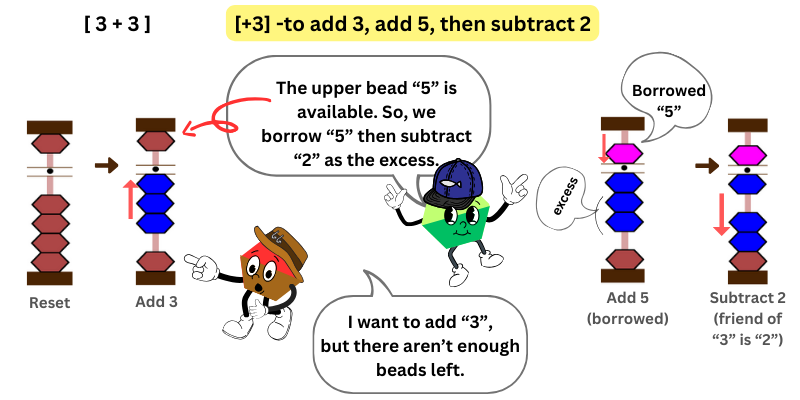
In this example, we want to add 3 + 3. We add 3 by moving 3 lower beads towards the bar.
We want to add 3 again, but there aren’t enough lower beads available. There is only 1 bead left. What shall we do?
We check if the upper bead 5 is available. Yes it’s available! Thus, we borrow the upper bead 5, and subtract the excess.
Do you know who is the friend of 3? That’s 2. So, we subtract 3.
For instance, in this example, you wanted to add 3. What is the next phrase?
To add add3, add 5, then subtract 2
Therefore, when you want to add 3 but not enough beads available, add (borrow) the upper bead 5, then subtract 2.
The 2 & 3 friend approach works just like the 1 & 4 friend approach.

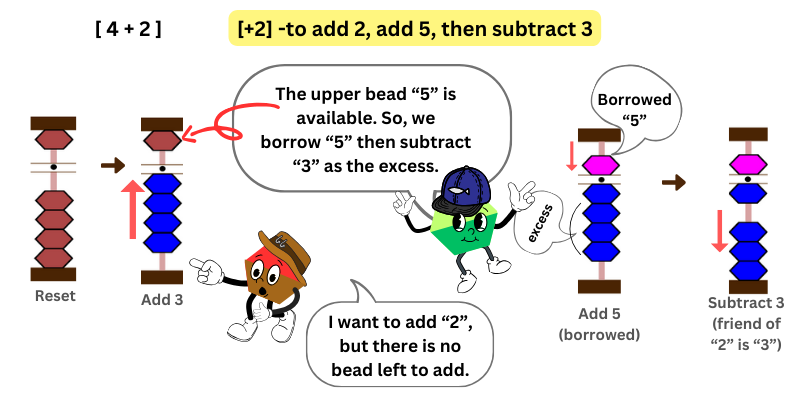
In this example, we want to add 4 + 2. We add 4 by moving 4 lower beads towards the bar.
Then, we want to add 2, but there is no bead left.
As we have learned in the previous examples, we check to see if the upper bead 5 is available.
If yes, add (borrow) the upper bead 5, and subtract the excess. What is the excess? That’s 3 – the 2’s friend.
For instance, in this example, you wanted to add 2. What is the next phrase?
To add 2, add 5, then subtract 3
Therefore, when you want to add 2 but no bead available, add (borrow) the upper bead 5, then subtract 3.
These friend approach is so useful that you should remember them.There is another friend approach to make “10” – we will get into the topic later.

The Friend Approach : Multi-digit
Let’s try out how the friend approach works for multi-digit addition.
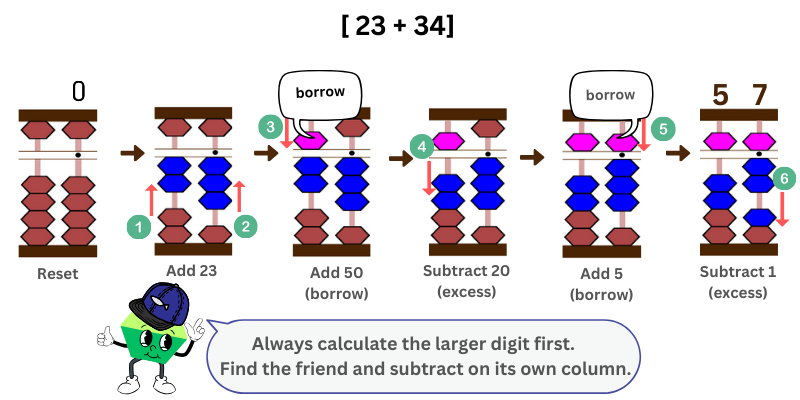
In this example, we want to add 23 + 34.For multi-digit number addition and subtraction, always begin with the one having the highest place value. In this example, start with the tens place column.
The first number is 23. Add 20 on the tens place column first, then add 3 on the ones place column.
Then, you want to add 34 on the abacus. Though we want to add 30 first, there are no enough lower beads in the tens column but the upper bead 5 is available. Therefore, we can apply the friend approach “to add 3, add 5 then subtract 2” in the tens column. For instance, in the tens column, add (borrow) 5, then subtract 2 (the excess).
Then moving onto the ones place column, you want to add 4 but there aren’t enough beads available. Since the upper bead 5 is available, we can use the friend approach “to add 4, add 1, then subtract 1”. In the ones column, add (borrow) 5, then subtract 1 (the excess).
Count the numbers on abacus. It’s 57. 23 + 34 = 57.

Please watch the lesson videos below (part 1 and part 2) to strengthen your understanding of the friend approach.
Video Lesson (Friend Approach for Addition)

Practice Questions
Work through all the worksheet or video questions multiple times until you feel confident with additions using the friend appeoach. Consistent practice will enhance your skills.
Click the green button below to access the printable worksheets.
Click below to access the video practice questions.


In this lesson, we introduced the friend approach for addition. The friends are pairs that make 5 together: 1 and 4, and 2 and 3. This method comes in handy when you’ve used up all the lower beads but still have the upper bead 5 available. We can borrow that upper bead 5 and give back the extra. That extra bit is actually the complement or the friend we’re talking about. We use the same friends for subtraction, but in a different way. We’ll dive into that in our next lesson.
You can find the friend approach sheet in PDF format on the worksheet page. Print it out and keep it nearby so you can refer to it while you’re working with the abacus.

