
Welcome to Abacus Lesson 10!
In our last lesson, we tackled addition with carryover, extending to the next place value column when the current one lacks sufficient beads. When this happens, we carry over 1 to the next column. For instance, if you’ve maxed out the ones column, you can add 10 more, but it’s crucial to subtract the excess. This process relies on the friend approach, specifically the 10-complement. Similar to the pairs that make 5 together, we now introduce pairs that make 10 together, aiding in carryover. The excess, or what we added too much, essentially becomes the friend, so subtracting it before adding 10 for the carryover is essential.
In this lesson, we delve into using the 10-complement approach for subtraction. If you lack sufficient beads to subtract, you can borrow from the higher place value. For instance, if you have 13 on the abacus and need to subtract 4, but there are only 3 beads in the ones column, you borrow “10” from the tens place. Of course, we need to add the difference we subtracted too much. The difference is its friend (complememnt of 10). Although we use the same friends (complements) as addition, we apply them differently.
Mastering the concepts of carrying over and borrowing for both 5 and 10 is pivotal in abacus learning. Make sure to thoroughly grasp these techniques for a solid foundation.

Subtraction with Borrowing
In this lesson, we will delve into subtraction with borrowing from the higher place value column. Consider having 14 on the abacus and wanting to subtract 7. Since there are only 4 beads in the ones place column, but there is a group of 10 in the tens column, we can borrow the 10. However, it’s essential to add the difference that we subtracted excessively. This difference can be computed by solving 10-7 or, alternatively, using the friend approach. Knowing that 7 and 3 make 10 together, when we want to subtract 7, we can subtract (borrow) 10 and add 3.
We rely on the same sets of friends to team up and make “10” together (1&9, 2&8, 3&7, 4&6, 5&5).
When we borrow from the next digit, there’s always a difference that needs to be added back.
While we could calculate this difference, remembering its pair that makes 10 makes it much simpler – it’s essentially the difference itself, eliminating the need for extra calculations.
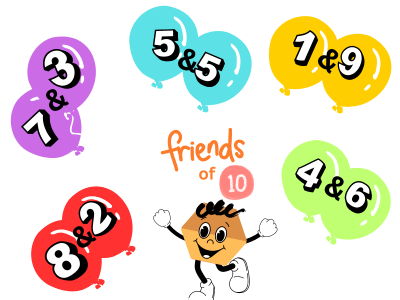

How to apply the friend approach when borrowing from the higher place value
If you need to take away a number in a specific column, let’s say the ones column, and there are no beads to subtract, what do you do? You borrow 1 bead (which is 10) from the tens place column and subtract from the 10. In these situations, you have to add back the difference that you subtracted too much.
For example, when doing the subtraction 12-8, you borrow 10 from the tens place column and then add back 2 as the difference that you subtracted too much.
Here are 9 combinations that make 10 together. If you remember these pairs, you’ll be able to use the friend approach right away. It’s a good idea to print them out along with “the friends that make 10 together” and keep them handy while you’re working on the abacus


When we carry over 1 to the next higher place value during addition, we subtract the excess (the friend) and then add 1 in the next higher place. However, in subtraction, it’s the opposite: we first subtract 10, and then add the difference (the friend). It’s important to note the different order in addition and subtraction. Let’s explore some examples below to see how the friend approach (10-complement) is used

The Friend Approach for Subtraction with Borrowing : 1 & 9
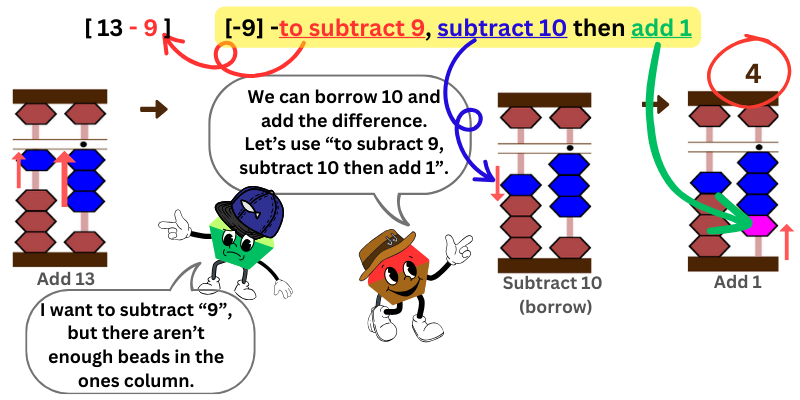
We will start by adding “13” on the abacus.
Next, we want to subtract “9,” but there are only 3 beads in the ones place column and we can’t subtract from there.
What’s the solution?
Refer to the table of “combinations to make 10 for subtraction.” Look for the entry “to subtract 9.” It says, “To subtract 9, subtract 10, then add 1.” We borrow “10” from the tens place column to subtract “9”, but we need to add back the difference “1” that we subtracted too much.
Count the number of beads attached at the bar. It’s 4. Thus, 13 – 9 = 4.

The Friend Approach for Subtraction with Borrowing : 2 & 8
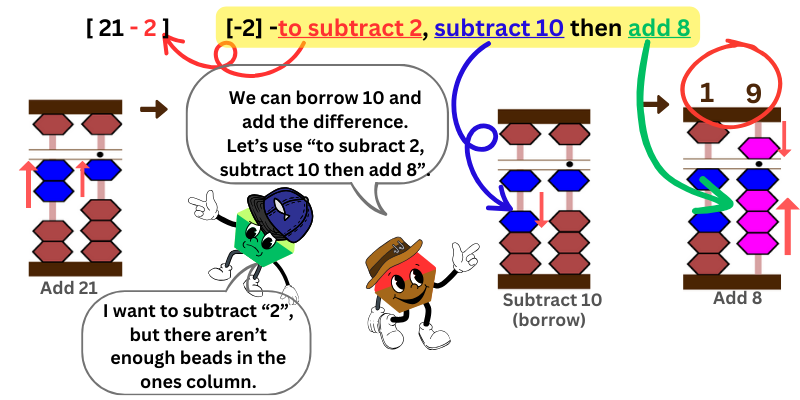
We first add “21” on the abacus.
Next, we want to subtract “9,” but there are only 1 bead in the ones place column and we can’t subtract from there.
What’s the solution?
Refer to the table of “combinations to make 10 for subtraction.” Look for the entry “to subtract 2.” It says, “To subtract 2, subtract 10, then add 8.” We borrow “10” from the tens place column to subtract “2”, but we need to add back the difference “8” that we subtracted too much.
Count the number of beads attached to the bar. It’s 19. 21 – 2 = 19.

The Friend Approach for Subtraction with Borrowing : 3 & 7
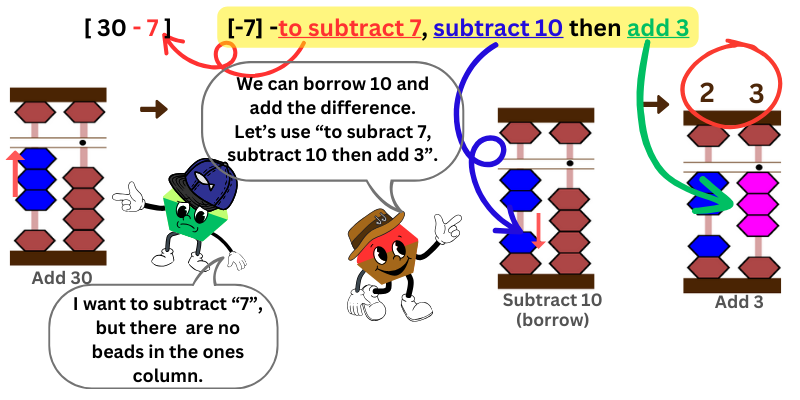
We first add “30” on the abacus.
Next, we want to subtract “7,” but there are no beads in the ones place column and we can’t subtract from there.
What’s the solution?
Refer to the table of “combinations to make 10 for subtraction.” Look for the entry “to subtract 7.” It says, “To subtract 7, subtract 10, then add 3.” We borrow “10” from the tens place column to subtract “7”, but we need to add back the difference “3” that we subtracted too much.
Count the number of beads attached at the bar. It’s 23. 30 – 7 = 23.

I hope you’re not feeling confused about using the friend approach for addition and subtraction. Recognizing the other pair is crucial, and so is the order. Mastering the friend approach for making 5 and making 10 is very important. Practice with worksheets as much as you can until you can do it faster and accurately

Lesson 10 video
Lesson 10 Practice Questions
Work through all the worksheet and video problems multiple times until you feel confident with subtraction with borrowing using the friend approach. Consistent practice will enhance your skills.


We’ve covered addition and subtraction, including carrying over and borrowing techniques. Next up, we’ll dive into multiplication and division (coming in fall 2024).
Make sure to practice as many questions as possible to become comfortable with calculating additions and subtractions, even with multi-digit numbers and various scenarios like carrying over and borrowing.
Mastering addition and subtraction is essential before moving on to multiplication. Keep practicing! You can find lesson videos and practice questions on my website. Happy learning with the abacus

